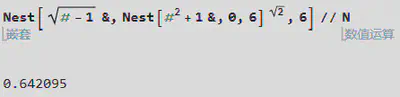A numerical probelm

Result calculated by J.

Firstly, note that $\lim_{x\rightarrow \infty}f(x)=x^{\sqrt{2}}$. So $x^{\sqrt{2}}$ is a good approximation while $x$ is sufficiently large. Firstly, we use following denotation

$$f^n(x)\triangleq\underbrace{f(f(f(\dots}_{x}0)\dots).$$

We can obtain:

$$f^{n+1}(0)\approx (f^{n}(0))^{\sqrt{2}}, n\in \mathbb{N}$$

Here, $n$ is large enough. And notice that $f^{2}(x)=x^2+1,\; f^{-2}(x)=\sqrt{x-1}$. Thus,

$$f(0)=f^{1}(0)=\lim_{n->\infty}f^{-2n}(\left(f^{2n}(0)\right)^{\sqrt{2}})$$

In fact, this approx converses very quickly. The error can be estimate as follows:

$$x^{\sqrt{2}}<f(x)<x^{\sqrt{2}}+1,$$ $$f^{2n+1}(0)-\left(f^{2n}(0)\right)^{\sqrt{2}}<1,$$ $$f^{2n-1}(0)-f^{-2}\left(\left(f^{2n}(0)\right)^{\sqrt{2}}\right)\approx 1\times\left.\frac{\mathrm{d} f^{-2}(x)}{\mathrm{d} x}\right|_{x=f^{2n}(0)}=\frac{1}{2 \sqrt{f^{2n}(0)-1}}=\frac{1}{2f^{2n-2}(0)},$$ $$f(0)-f^{-2n}\left(\left(f^{2n}(0)\right)^{\sqrt{2}}\right)\approx \frac{1}{2f^{2n-2}(0)}\frac{1}{2f^{2n-4}(0)}\dots\frac{1}{2f^{2}(0)}.$$ $$\lim_{n\rightarrow \infty} f^{2n}(0) =C^{2^n},$$

Thus the error is

$$O\left(\frac{1}{2^n C^{2^{4^{n-1}/3}}}\right)$$

, where $C\approx 1.22590244352$ is a constant.

Mathematica Code: